Decision Tree Regressor

π·π‘’π‘π‘–π‘ π‘–π‘œπ‘› π‘‡π‘Ÿπ‘’π‘’ π‘π‘™π‘Žπ‘ π‘ π‘–π‘“π‘–π‘’π‘Ÿ π‘‘β„Žπ‘’ π‘šπ‘Žπ‘–π‘› π‘”π‘œπ‘Žπ‘™ 𝑖𝑠 𝑓𝑖𝑛𝑑 π‘‘β„Žπ‘’ π‘Ÿπ‘œπ‘œπ‘‘ π‘›π‘œπ‘‘π‘’
● πΈπ‘›π‘‘π‘Ÿπ‘œπ‘π‘¦
● 𝐺𝑖𝑛𝑖
π·π‘’π‘π‘–π‘ π‘–π‘œπ‘› π‘‡π‘Ÿπ‘’π‘’ π‘Ÿπ‘’π‘”π‘Ÿπ‘’π‘ π‘ π‘œπ‘Ÿ π‘‘β„Žπ‘’ π‘šπ‘Žπ‘–π‘› π‘”π‘œπ‘Žπ‘™ 𝑖𝑠 𝑓𝑖𝑛𝑑 π‘‘β„Žπ‘’ π‘Ÿπ‘œπ‘œπ‘‘ π‘›π‘œπ‘‘π‘’
πΆπ‘Žπ‘™π‘π‘’π‘™π‘Žπ‘‘π‘’ π‘‘β„Žπ‘’ 𝑀𝑆𝐸 π‘Žπ‘‘ π‘‘π‘–π‘“π‘“π‘’π‘Ÿπ‘’π‘›π‘‘ π‘ π‘π‘™π‘œπ‘‘π‘ 
π‘₯ 𝑦
2 10
4 20
6 30
8 40
𝑆𝑑𝑒𝑝 βˆ’ 1: 𝑠𝑝𝑙𝑖𝑑 π‘‘β„Žπ‘’ π‘₯ π‘Žπ‘‘ π‘‘π‘–π‘“π‘“π‘’π‘Ÿπ‘’π‘›π‘‘ 𝑙𝑒𝑣𝑒𝑙𝑠
● π‘₯β‰₯3 π‘œπ‘Ÿ π‘₯ < 3

● π‘₯β‰₯5 π‘œπ‘Ÿ π‘₯ < 5

● π‘₯β‰₯6 π‘œπ‘Ÿ π‘₯ < 6 𝑆𝑑𝑒𝑝 βˆ’ 2: 𝑙𝑒𝑑𝑠 π‘€π‘œπ‘Ÿπ‘˜ π‘œπ‘› 𝑠𝑝𝑙𝑖𝑑 π‘Žπ‘‘ 5

● π‘₯≀ 5 π‘›π‘’π‘šπ‘π‘’π‘Ÿ π‘œπ‘“ π‘œπ‘π‘  = 2 𝑖𝑛𝑝𝑒𝑑𝑠 = [2, 4] π‘œπ‘’π‘‘π‘π‘’π‘‘(𝑦) = [10, 20]

● π‘¦π‘šπ‘’π‘Žπ‘› =10+202 = 15

● π‘šπ‘ π‘’1 =(10βˆ’15)2+(20βˆ’15)22 = 25

● π‘₯ > 5 π‘›π‘’π‘šπ‘π‘’π‘Ÿ π‘œπ‘“ π‘œπ‘π‘  = 2 𝑖𝑛𝑝𝑒𝑑𝑠 = [6, 8] π‘œπ‘’π‘‘π‘π‘’π‘‘(𝑦) = [30, 40]
● π‘¦π‘šπ‘’π‘Žπ‘› =30+402 = 35
● π‘šπ‘ π‘’2 =(30βˆ’35)2+(40βˆ’35)22
= 25
𝑆𝑑𝑒𝑝 βˆ’ 3: π‘‡π‘œπ‘‘π‘Žπ‘™ π‘šπ‘ π‘’ = 𝑀1* π‘šπ‘ π‘’1 + 𝑀2* π‘šπ‘ π‘’2
𝑀1 = π‘€β„Žπ‘’π‘› π‘₯≀5 π‘‘π‘€π‘œ 𝑖𝑛𝑝𝑒𝑑 π‘œπ‘π‘ π‘’π‘Ÿπ‘£π‘Žπ‘‘π‘–π‘œπ‘› π‘Žπ‘Ÿπ‘’ π‘Žπ‘£π‘Žπ‘–π‘™π‘Žπ‘π‘™π‘’ π‘œπ‘’π‘‘ π‘œπ‘“ π‘‘π‘œπ‘‘π‘Žπ‘™ (4) =24
𝑀2 = π‘€β„Žπ‘’π‘› π‘₯ > 5 π‘‘π‘€π‘œ 𝑖𝑛𝑝𝑒𝑑 π‘œπ‘π‘ π‘’π‘Ÿπ‘£π‘Žπ‘‘π‘–π‘œπ‘› π‘Žπ‘Ÿπ‘’ π‘Žπ‘£π‘Žπ‘–π‘™π‘Žπ‘π‘™π‘’ π‘œπ‘’π‘‘ π‘œπ‘“ π‘‘π‘œπ‘‘π‘Žπ‘™ (4) =24
π‘‡π‘œπ‘‘π‘Žπ‘™ π‘šπ‘ π‘’ =24* 25 +24* 25
π‘Ÿπ‘’π‘π‘’π‘Žπ‘‘ π‘‘β„Žπ‘’ π‘ π‘Žπ‘šπ‘’ 𝑠𝑑𝑒𝑝𝑠 π‘“π‘œπ‘Ÿ π‘₯ = 3 π‘₯ = 7 π‘Žπ‘›π‘‘ π‘ π‘œ π‘œπ‘›
π‘π‘œπ‘›π‘π‘™π‘’π‘ π‘–π‘œπ‘› : π‘€β„Žπ‘–π‘β„Ž 𝑠𝑝𝑙𝑖𝑑 β„Žπ‘Žπ‘  π‘™π‘œπ‘€π‘’π‘ π‘‘ 𝑀𝑆𝐸 π‘‘β„Žπ‘Žπ‘‘ π‘π‘’π‘π‘œπ‘šπ‘’ π‘Ž 𝑏𝑒𝑠𝑑 𝑠𝑝𝑙𝑖𝑑 π‘œπ‘› π‘‘β„Žπ‘–π‘  π‘π‘œπ‘™π‘’π‘šπ‘›
π‘Žπ‘ π‘ π‘’π‘šπ‘’ π‘‘β„Žπ‘Žπ‘‘ π‘₯ = 5 𝑀𝑒 β„Žπ‘Žπ‘£π‘’ π‘Ž π‘™π‘œπ‘€ π‘šπ‘ π‘’ π‘‘β„Žπ‘–π‘  π‘π‘’π‘π‘œπ‘šπ‘’ 𝑏𝑒𝑠𝑑 𝑠𝑝𝑙𝑖𝑑 π‘“π‘œπ‘Ÿ π‘‘β„Žπ‘–π‘  π‘π‘œπ‘™π‘’π‘šπ‘›
𝑒π‘₯π‘Žπ‘šπ‘π‘™π‘’ : π‘ π‘žπ‘“π‘‘ , π‘‘π‘–π‘ π‘‘π‘Žπ‘›π‘π‘’, π‘–π‘›π‘π‘œπ‘šπ‘’
π‘π‘Žπ‘™π‘π‘’π‘™π‘Žπ‘‘π‘’ π‘™π‘œπ‘€ π‘šπ‘ π‘’ π‘Žπ‘‘ π‘’π‘Žπ‘β„Ž π‘π‘œπ‘ π‘ π‘–π‘π‘™π‘’ 𝑠𝑝𝑙𝑖𝑑𝑠 π‘“π‘œπ‘Ÿ π‘–π‘›π‘π‘œπ‘šπ‘’(π‘Žπ‘ π‘ π‘’π‘šπ‘’ 50 π‘–π‘›π‘‘π‘’π‘Ÿπ‘›π‘Žπ‘™ 𝑠𝑝𝑙𝑖𝑑𝑠)
π‘π‘Žπ‘™π‘π‘’π‘™π‘Žπ‘‘π‘’ π‘™π‘œπ‘€ π‘šπ‘ π‘’ π‘Žπ‘‘ π‘’π‘Žπ‘β„Ž π‘π‘œπ‘ π‘ π‘–π‘π‘™π‘’ 𝑠𝑝𝑙𝑖𝑑𝑠 π‘“π‘œπ‘Ÿ π‘‘π‘–π‘ π‘‘π‘Žπ‘›π‘π‘’ (π‘Žπ‘ π‘ π‘’π‘šπ‘’ 100)
π‘π‘Žπ‘™π‘π‘’π‘™π‘Žπ‘‘π‘’ π‘™π‘œπ‘€ π‘šπ‘ π‘’ π‘Žπ‘‘ π‘’π‘Žπ‘β„Ž π‘π‘œπ‘ π‘ π‘–π‘π‘™π‘’ 𝑠𝑝𝑙𝑖𝑑𝑠 π‘“π‘œπ‘Ÿ π‘ π‘žπ‘“π‘‘(π‘Žπ‘ π‘ π‘’π‘šπ‘’ 10 )
π‘œπ‘’π‘‘ π‘œπ‘“ π‘‘β„Žπ‘’π‘ π‘’ 3 π‘€β„Žπ‘–π‘β„Ž 𝑖𝑠 π‘Žπ‘”π‘Žπ‘–π‘› π‘™π‘œπ‘€π‘’π‘ π‘‘ π‘‘β„Žπ‘Žπ‘‘ π‘π‘’π‘π‘œπ‘šπ‘’ π‘Ž π‘Ÿπ‘œπ‘œπ‘‘ π‘›π‘œπ‘‘π‘’

class sklearn.tree.DecisionTreeRegressor(*, criterion=’squared_error’, splitter=’best’, max_depth=None, min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_features=None, random_state=None, max_leaf_nodes=None, min_impurity_decrease=0.0, ccp_alpha=0.0, monotonic_cst=None)[source]

A decision tree regressor.

Read more in the User Guide.Parameters:criterion{β€œsquared_error”, β€œfriedman_mse”, β€œabsolute_error”, β€œpoisson”}, default=”squared_error”

The function to measure the quality of a split. Supported criteria are β€œsquared_error” for the mean squared error, which is equal to variance reduction as feature selection criterion and minimizes the L2 loss using the mean of each terminal node, β€œfriedman_mse”, which uses mean squared error with Friedman’s improvement score for potential splits, β€œabsolute_error” for the mean absolute error, which minimizes the L1 loss using the median of each terminal node, and β€œpoisson” which uses reduction in the half mean Poisson deviance to find splits.

Added in version 0.18: Mean Absolute Error (MAE) criterion.

Added in version 0.24: Poisson deviance criterion.splitter{β€œbest”, β€œrandom”}, default=”best”

The strategy used to choose the split at each node. Supported strategies are β€œbest” to choose the best split and β€œrandom” to choose the best random split.max_depthint, default=None

The maximum depth of the tree. If None, then nodes are expanded until all leaves are pure or until all leaves contain less than min_samples_split samples.

For an example of how max_depth influences the model, see Decision Tree Regression.min_samples_splitint or float, default=2

The minimum number of samples required to split an internal node:

  • If int, then considerΒ min_samples_splitΒ as the minimum number.
  • If float, thenΒ min_samples_splitΒ is a fraction andΒ ceil(min_samples_splitΒ *Β n_samples)Β are the minimum number of samples for each split.

Changed in version 0.18: Added float values for fractions.min_samples_leafint or float, default=1

The minimum number of samples required to be at a leaf node. A split point at any depth will only be considered if it leaves at least min_samples_leaf training samples in each of the left and right branches. This may have the effect of smoothing the model, especially in regression.

  • If int, then considerΒ min_samples_leafΒ as the minimum number.
  • If float, thenΒ min_samples_leafΒ is a fraction andΒ ceil(min_samples_leafΒ *Β n_samples)Β are the minimum number of samples for each node.

Changed in version 0.18: Added float values for fractions.min_weight_fraction_leaffloat, default=0.0

The minimum weighted fraction of the sum total of weights (of all the input samples) required to be at a leaf node. Samples have equal weight when sample_weight is not provided.max_featuresint, float or {β€œsqrt”, β€œlog2”}, default=None

The number of features to consider when looking for the best split:

  • If int, then considerΒ max_featuresΒ features at each split.
  • If float, thenΒ max_featuresΒ is a fraction andΒ max(1,Β int(max_featuresΒ *Β n_features_in_))Β features are considered at each split.
  • If β€œsqrt”, thenΒ max_features=sqrt(n_features).
  • If β€œlog2”, thenΒ max_features=log2(n_features).
  • If None, thenΒ max_features=n_features.

Note: the search for a split does not stop until at least one valid partition of the node samples is found, even if it requires to effectively inspect more than max_features features.random_stateint, RandomState instance or None, default=None

Controls the randomness of the estimator. The features are always randomly permuted at each split, even if splitter is set to "best". When max_features < n_features, the algorithm will select max_features at random at each split before finding the best split among them. But the best found split may vary across different runs, even if max_features=n_features. That is the case, if the improvement of the criterion is identical for several splits and one split has to be selected at random. To obtain a deterministic behaviour during fitting, random_state has to be fixed to an integer. See Glossary for details.max_leaf_nodesint, default=None

Grow a tree with max_leaf_nodes in best-first fashion. Best nodes are defined as relative reduction in impurity. If None then unlimited number of leaf nodes.min_impurity_decreasefloat, default=0.0

A node will be split if this split induces a decrease of the impurity greater than or equal to this value.

The weighted impurity decrease equation is the following:

N_t / N * (impurity - N_t_R / N_t * right_impurity
                    - N_t_L / N_t * left_impurity)

where N is the total number of samples, N_t is the number of samples at the current node, N_t_L is the number of samples in the left child, and N_t_R is the number of samples in the right child.

N, N_t, N_t_R and N_t_L all refer to the weighted sum, if sample_weight is passed.

Added in version 0.19.ccp_alphanon-negative float, default=0.0

Complexity parameter used for Minimal Cost-Complexity Pruning. The subtree with the largest cost complexity that is smaller than ccp_alpha will be chosen. By default, no pruning is performed. See Minimal Cost-Complexity Pruning for details. See Post pruning decision trees with cost complexity pruning for an example of such pruning.

Added in version 0.22.monotonic_cstarray-like of int of shape (n_features), default=NoneIndicates the monotonicity constraint to enforce on each feature.

  • 1: monotonic increase
  • 0: no constraint
  • -1: monotonic decrease

If monotonic_cst is None, no constraints are applied.Monotonicity constraints are not supported for:

  • multioutput regressions (i.e. whenΒ n_outputs_Β >Β 1),
  • regressions trained on data with missing values.

Read more in the User Guide.

Added in version 1.4.Attributes:feature_importances_ndarray of shape (n_features,)

Return the feature importances.max_features_int

The inferred value of max_features.n_features_in_int

Number of features seen during fit.

Added in version 0.24.feature_names_in_ndarray of shape (n_features_in_,)

Names of features seen during fit. Defined only when X has feature names that are all strings.

Added in version 1.0.n_outputs_int

The number of outputs when fit is performed.tree_Tree instance

The underlying Tree object. Please refer to help(sklearn.tree._tree.Tree) for attributes of Tree object and Understanding the decision tree structure for basic usage of these attributes.

Decision Trees are everywhere in machine learning, beloved for their intuitive output. Who doesn’t love a simple “if-then” flowchart? Despite their popularity, it’s surprising how challenging it is to find a clear, step-by-step explanation of how Decision Trees work. (I’m actually embarrassed by how long it took me to actually understand how the algorithm works.)

So, in this breakdown, I’ll be focusing on the essentials of tree construction. We’ll unpack exactly what’s happening in each node and why, from root to final leaves (with visuals of course).

All visuals: Author-created using Canva Pro. Optimized for mobile; may appear oversized on desktop.
All visuals: Author-created using Canva Pro. Optimized for mobile; may appear oversized on desktop.

Definition

A Decision Tree classifier creates an upside-down tree to make predictions, starting at the top with a question about an important feature in your data, then branches out based on the answers. As you follow these branches down, each stop asks another question, narrowing down the possibilities. This question-and-answer game continues until you reach the bottom – a leaf node – where you get your final prediction or classification.

Decision Tree is one of the most important machine learning algorithms - it's a series of yes or no question.
Decision Tree is one of the most important machine learning algorithms – it’s a series of yes or no question.

Dataset Used

Throughout this article, we’ll use this artificial golf dataset (inspired by [1]) as an example. This dataset predicts whether a person will play golf based on weather conditions.

Columns: 'Outlook' (already one-hot encoded to sunny, overcast, rainy), 'Temperature' (in Fahrenheit), 'Humidity' (in %), 'Wind' (yes/no), and 'Play' (target feature)
Columns: β€˜Outlook’ (already one-hot encoded to sunny, overcast, rainy), β€˜Temperature’ (in Fahrenheit), β€˜Humidity’ (in %), β€˜Wind’ (yes/no), and β€˜Play’ (target feature)

Import libraries

from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
import pandas as pd
import numpy as np

Load data

dataset_dict = {
‘Outlook’: [‘sunny’, ‘sunny’, ‘overcast’, ‘rainy’, ‘rainy’, ‘rainy’, ‘overcast’, ‘sunny’, ‘sunny’, ‘rainy’, ‘sunny’, ‘overcast’, ‘overcast’, ‘rainy’, ‘sunny’, ‘overcast’, ‘rainy’, ‘sunny’, ‘sunny’, ‘rainy’, ‘overcast’, ‘rainy’, ‘sunny’, ‘overcast’, ‘sunny’, ‘overcast’, ‘rainy’, ‘overcast’],
‘Temperature’: [85.0, 80.0, 83.0, 70.0, 68.0, 65.0, 64.0, 72.0, 69.0, 75.0, 75.0, 72.0, 81.0, 71.0, 81.0, 74.0, 76.0, 78.0, 82.0, 67.0, 85.0, 73.0, 88.0, 77.0, 79.0, 80.0, 66.0, 84.0],
‘Humidity’: [85.0, 90.0, 78.0, 96.0, 80.0, 70.0, 65.0, 95.0, 70.0, 80.0, 70.0, 90.0, 75.0, 80.0, 88.0, 92.0, 85.0, 75.0, 92.0, 90.0, 85.0, 88.0, 65.0, 70.0, 60.0, 95.0, 70.0, 78.0],
‘Wind’: [False, True, False, False, False, True, True, False, False, False, True, True, False, True, True, False, False, True, False, True, True, False, True, False, False, True, False, False],
‘Play’: [‘No’, ‘No’, ‘Yes’, ‘Yes’, ‘Yes’, ‘No’, ‘Yes’, ‘No’, ‘Yes’, ‘Yes’, ‘Yes’, ‘Yes’, ‘Yes’, ‘No’, ‘No’, ‘Yes’, ‘Yes’, ‘No’, ‘No’, ‘No’, ‘Yes’, ‘Yes’, ‘Yes’, ‘Yes’, ‘Yes’, ‘Yes’, ‘No’, ‘Yes’]
}
df = pd.DataFrame(dataset_dict)

Preprocess data

df = pd.get_dummies(df, columns=[‘Outlook’], prefix=”, prefix_sep=”, dtype=int)
df[‘Wind’] = df[‘Wind’].astype(int)
df[‘Play’] = (df[‘Play’] == ‘Yes’).astype(int)

Reorder the columns

df = df[[‘sunny’, ‘overcast’, ‘rainy’, ‘Temperature’, ‘Humidity’, ‘Wind’, ‘Play’]]

Prepare features and target

X, y = df.drop(columns=’Play’), df[‘Play’]

Split data

X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.5, shuffle=False)

Display results

print(pd.concat([X_train, y_train], axis=1), ‘n’)
print(pd.concat([X_test, y_test], axis=1))

Main Mechanism

The Decision Tree classifier operates by recursively splitting the data based on the most informative features. Here’s how it works:

  1. Start with the entire dataset at the root node.
  2. Select the best feature to split the data (based on measures like Gini impurity).
  3. Create child nodes for each possible value of the selected feature.
  4. Repeat steps 2–3 for each child node until a stopping criterion is met (e.g., maximum depth reached, minimum samples per leaf, or pure leaf nodes).
  5. Assign the majority class to each leaf node.

Training Steps

In scikit-learn, the decision tree algorithm is called CART (Classification and Regression Trees). It builds binary trees and typically follows these steps:

  1. Start with all training samples in the root node.
Starting with the root node containing all 14 training samples, we will figure out the best way feature and the best point to split the data to start building the tree.
Starting with the root node containing all 14 training samples, we will figure out the best way feature and the best point to split the data to start building the tree.

2.For each feature: a. Sort the feature values. b. Consider all possible thresholds between adjacent values as potential split points.

In this root node, there are 23 split points to check. Binary columns only has one split point.
In this root node, there are 23 split points to check. Binary columns only has one split point.

def potential_split_points(attr_name, attr_values):
sorted_attr = np.sort(attr_values)
unique_values = np.unique(sorted_attr)
split_points = [(unique_values[i] + unique_values[i+1]) / 2 for i in range(len(unique_values) – 1)]
return {attr_name: split_points}

Calculate and display potential split points for all columns

for column in X_train.columns:
splits = potential_split_points(column, X_train[column])
for attr, points in splits.items():
print(f”{attr:11}: {points}”)

  1. Create two child nodes based on the chosen feature and split point:
    • Left child: samples with feature value <= split point
    • Right child: samples with feature value > split point
The selected split point split the data into two parts. As one part already pure (the right side! That's why it's impurity is low!), we only need to continue the tree on the left node.
The selected split point split the data into two parts. As one part already pure (the right side! That’s why it’s impurity is low!), we only need to continue the tree on the left node.
  1. Recursively repeat steps 2–5 for each child node. You can also stop until a stopping criterion is met (e.g., maximum depth reached, minimum number of samples per leaf node, or minimum impurity decrease).

Final Complete Tree

The class label of a leaf node is the majority class of the training samples that reached that node.

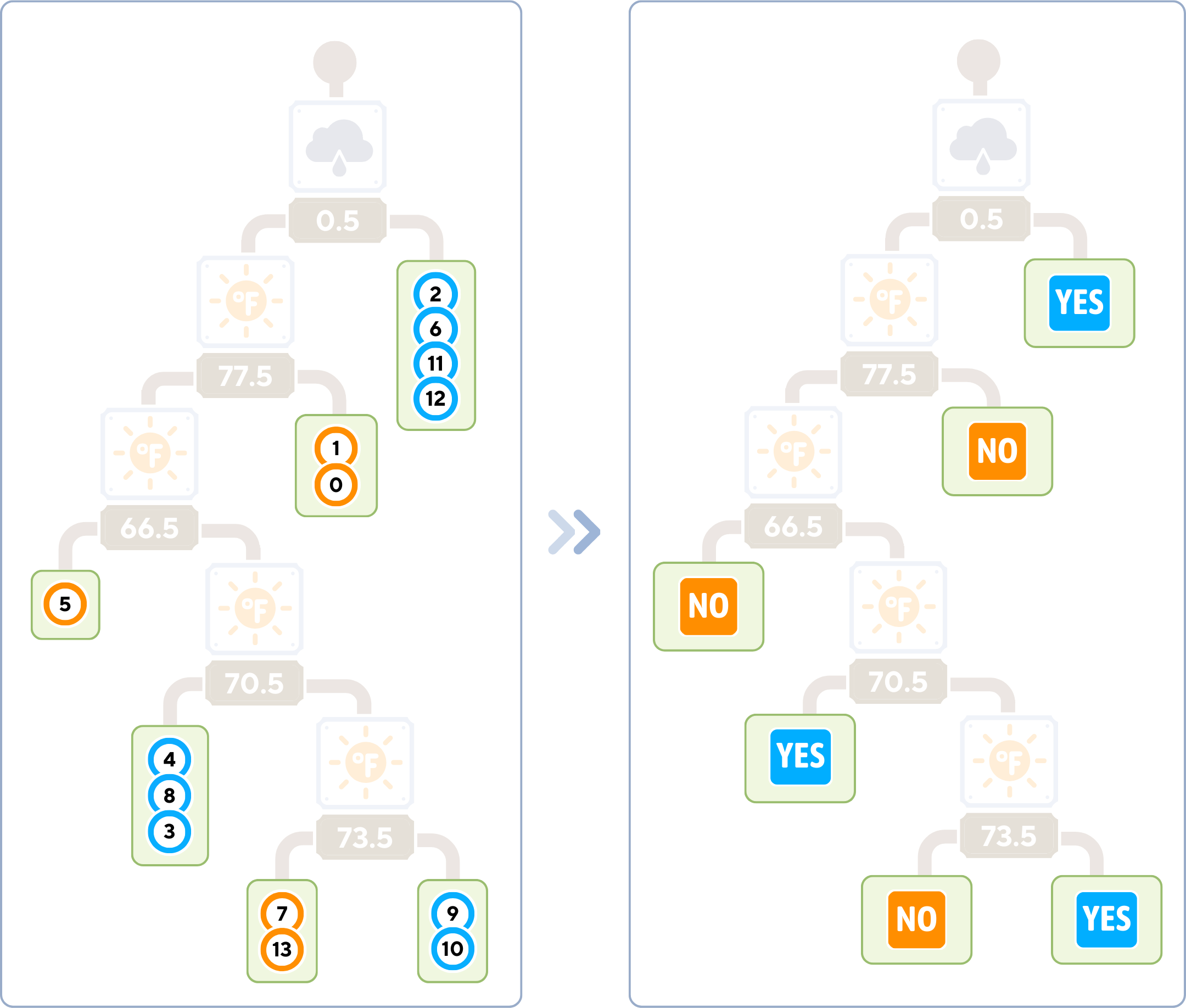
The right one is the final tree that will be used for classification. We do not need the samples anymore at this point.
The right one is the final tree that will be used for classification. We do not need the samples anymore at this point.
The decision tree gives an adequate accuracy. As our tree only checks two features, it might not capture the test set characteristic well.
The decision tree gives an adequate accuracy. As our tree only checks two features, it might not capture the test set characteristic well.
# Evaluate the classifier
print(f"Accuracy: {accuracy_score(y_test, y_pred)}")

Key Parameters

Decision Trees have several important parameters that control their growth and complexity:

1 . Max Depth: This sets the maximum depth of the tree, which can be a valuable tool in preventing overfitting.

 Helpful Tip: Consider starting with a shallow tree (perhaps 3–5 levels deep) and gradually increasing the depth.

Start with a shallow tree (e.g., depth of 3–5) and gradually increase until you find the optimal balance between model complexity and performance on validation data.
Start with a shallow tree (e.g., depth of 3–5) and gradually increase until you find the optimal balance between model complexity and performance on validation data.
  1. Min Samples Split: This parameter determines the minimum number of samples needed to split an internal node.

 Helpful Tip: Setting this to a higher value (around 5–10% of your training data) can help prevent the tree from creating too many small, specific splits that might not generalize well to new data.

  1. Min Samples Leaf: This specifies the minimum number of samples required at a leaf node.

 Helpful Tip: Choose a value that ensures each leaf represents a meaningful subset of your data (approximately 1–5% of your training data). This can help avoid overly specific predictions.

Pros & Cons

Like any algorithm in machine learning, Decision Trees have their strengths and limitations.

Pros:

  1. Interpretability: Easy to understand and visualize the decision-making process.
  2. No Feature Scaling: Can handle both numerical and categorical data without normalization.
  3. Handles Non-linear Relationships: Can capture complex patterns in the data.
  4. Feature Importance: Provides a clear indication of which features are most important for prediction.

Cons:

  1. Overfitting: Prone to creating overly complex trees that don’t generalize well, especially with small datasets.
  2. Instability: Small changes in the data can result in a completely different tree being generated.
  3. Biased with Imbalanced Datasets: Can be biased towards dominant classes.
  4. Inability to Extrapolate: Cannot make predictions beyond the range of the training data.

In our golf example, a Decision Tree might create very accurate and interpretable rules for deciding whether to play golf based on weather conditions. However, it might overfit to specific combinations of conditions if not properly pruned or if the dataset is small.

Final Remarks

Decision Tree Classifiers are a great tool for solving many types of problems in machine learning. They’re easy to understand, can handle complex data, and show us how they make decisions. This makes them useful in many areas, from business to medicine. While Decision Trees are powerful and interpretable, they’re often used as building blocks for more advanced ensemble methods like Random Forests or Gradient Boosting Machines.

Load data

dataset_dict = {
‘Outlook’: [‘sunny’, ‘sunny’, ‘overcast’, ‘rainy’, ‘rainy’, ‘rainy’, ‘overcast’, ‘sunny’, ‘sunny’, ‘rainy’, ‘sunny’, ‘overcast’, ‘overcast’, ‘rainy’, ‘sunny’, ‘overcast’, ‘rainy’, ‘sunny’, ‘sunny’, ‘rainy’, ‘overcast’, ‘rainy’, ‘sunny’, ‘overcast’, ‘sunny’, ‘overcast’, ‘rainy’, ‘overcast’],
‘Temperature’: [85.0, 80.0, 83.0, 70.0, 68.0, 65.0, 64.0, 72.0, 69.0, 75.0, 75.0, 72.0, 81.0, 71.0, 81.0, 74.0, 76.0, 78.0, 82.0, 67.0, 85.0, 73.0, 88.0, 77.0, 79.0, 80.0, 66.0, 84.0],
‘Humidity’: [85.0, 90.0, 78.0, 96.0, 80.0, 70.0, 65.0, 95.0, 70.0, 80.0, 70.0, 90.0, 75.0, 80.0, 88.0, 92.0, 85.0, 75.0, 92.0, 90.0, 85.0, 88.0, 65.0, 70.0, 60.0, 95.0, 70.0, 78.0],
‘Wind’: [False, True, False, False, False, True, True, False, False, False, True, True, False, True, True, False, False, True, False, True, True, False, True, False, False, True, False, False],
‘Play’: [‘No’, ‘No’, ‘Yes’, ‘Yes’, ‘Yes’, ‘No’, ‘Yes’, ‘No’, ‘Yes’, ‘Yes’, ‘Yes’, ‘Yes’, ‘Yes’, ‘No’, ‘No’, ‘Yes’, ‘Yes’, ‘No’, ‘No’, ‘No’, ‘Yes’, ‘Yes’, ‘Yes’, ‘Yes’, ‘Yes’, ‘Yes’, ‘No’, ‘Yes’]
}
df = pd.DataFrame(dataset_dict)

Prepare data

df = pd.get_dummies(df, columns=[‘Outlook’], prefix=”, prefix_sep=”, dtype=int)
df[‘Wind’] = df[‘Wind’].astype(int)
df[‘Play’] = (df[‘Play’] == ‘Yes’).astype(int)

Split data

X, y = df.drop(columns=’Play’), df[‘Play’]
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.5, shuffle=False)

Train model

dt_clf = DecisionTreeClassifier(
max_depth=None, # Maximum depth of the tree
min_samples_split=2, # Minimum number of samples required to split an internal node
min_samples_leaf=1, # Minimum number of samples required to be at a leaf node
criterion=’gini’ # Function to measure the quality of a split
)
dt_clf.fit(X_train, y_train)

Make predictions

y_pred = dt_clf.predict(X_test)

Evaluate model

print(f”Accuracy: {accuracy_score(y_test, y_pred)}”)

Visualize tree

plt.figure(figsize=(20, 10))
plot_tree(dt_clf, filled=True, feature_names=X.columns,
class_names=[‘Not Play’, ‘Play’], impurity=False)
plt.show()

kamblenayan826

Leave a Reply

Your email address will not be published. Required fields are marked *